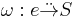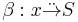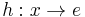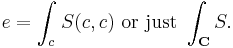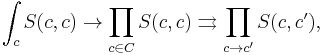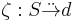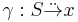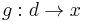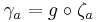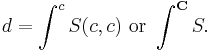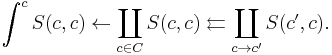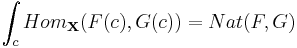End (category theory)
In category theory, an end of a functor 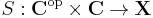 is a universal dinatural transformation from an object e of X to S.
is a universal dinatural transformation from an object e of X to S.
More explicitly, this is a pair 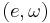 , where e is an object of X and
, where e is an object of X and
is a dinatural transformation from the constant functor whose value is e on every object and 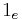 on every morphism, such that for every dinatural transformation
on every morphism, such that for every dinatural transformation
there exists a unique morphism
of X with
for every object a of C.
By abuse of language the object e is often called the end of the functor S (forgetting  ) and is written
) and is written
If X is complete, the end can be described as the equalizer in the diagram
where the first morphism is induced by 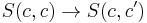 and the second morphism is induced by
and the second morphism is induced by 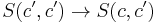 .
.
Coend
The definition of the coend of a functor 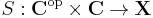 is the dual of the definition of an end.
is the dual of the definition of an end.
Thus, a coend of S consists of a pair 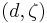 , where d is an object of X and
, where d is an object of X and
is a dinatural transformation, such that for every dinatural transformation
there exists a unique morphism
of X with
for every object a of C.
The coend d of the functor S is written
Dually, if X is cocomplete, then the coend can be described as the coequalizer in the diagram
Examples
Suppose we have functors 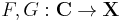 then
then 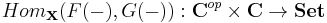 . In this case, the category of sets is complete, so we need only form the equalizer and in this case
. In this case, the category of sets is complete, so we need only form the equalizer and in this case
the natural transformations from  to
to  . Intuitively, a natural transformation from
. Intuitively, a natural transformation from  to
to  is a morphism from
is a morphism from 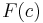 to
to 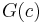 for every
for every  in the category with compatibility conditions. Looking at the equalizer diagram defining the end makes the equivalence clear.
in the category with compatibility conditions. Looking at the equalizer diagram defining the end makes the equivalence clear.
Let  be a simplicial set. That is,
be a simplicial set. That is,  is a functor
is a functor 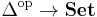 . The Discrete topology gives a functor
. The Discrete topology gives a functor 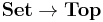 , where
, where 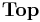 is the category of topological spaces. Moreover, there is a map
is the category of topological spaces. Moreover, there is a map 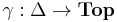 which sends the object
which sends the object ![[n]](/2012-wikipedia_en_all_nopic_01_2012/I/de504dafb2a07922de5e25813d0aaafd.png) of
of  to the standard
to the standard  simplex inside
simplex inside 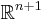 . Finally there is a functor
. Finally there is a functor 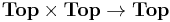 which takes the product of two topological spaces. Define
which takes the product of two topological spaces. Define  to be the composition of this product functor with
to be the composition of this product functor with 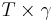 . The coend of
. The coend of  is the geometric realization of
is the geometric realization of  .
.